2025年秋现代优化技术
数据挖掘部分
关联规则——Apriori算法
关联规则
关联规则,就是发现数据中不同物品或事件之间“经常一起出现”的规律。它回答的问题是:如果顾客买了A,那么他很可能也会买B。最著名的故事就是 “啤酒与尿布”:超市通过分析销售数据发现,每周五晚上,很多男性顾客在买尿布的同时,也会顺便买啤酒。于是,超市就把啤酒和尿布摆放在一起,结果两者的销量都大幅增加。这条规律——“买尿布→买啤酒”,就是一条关联规则。一条规则通常写成:X→Y如果X发生,那么Y也可能发生,例如 {牛奶,面包} → {鸡蛋}就表示如果一个顾客买了牛奶和面包,那他就很有可能同时买鸡蛋。关联规则的形式是 X → Y,其中X和Y都是项集。要判断一个规则是否有效,首先需要X∪Y(整个项集)是频繁的。如果连整个项集都不经常出现,那么基于它的规则就没有统计意义。 其次,我们还需要关注一条规则是否可靠。为此,引入两个概念:
- 项集x的支持度sup(x):
。支持度表示项集出现的频率,它可以反映一个项集是否具有统计意义,我们会人为设定一个最小支持度,如果项集的支持度大于该最小支持度就说这个项集是频繁的,也就是说它是有统计学意义的。 - 关联规则x→y的置信度con(x→y):
。置信度表示项集x出现的情况下y也同时出现的概率,它反映一个关联规则是否可靠,我们会人为设定一个最小置信度,如果关联规则的置信度大于该最小置信度就说这个关联规则是可靠的。例如con({牛奶,面包}→{鸡蛋})=0.75的含义就是买{牛奶,面包}的情况下有75%的概率还会买鸡蛋,如果我们的最小置信度是0.7,那么这条关联规则就是可靠的,因为我们确实有70%以上的把握认为顾客买了牛奶和面包后还会买鸡蛋。
但是,还不够完美,一种情况是con(x→y)很大的原因是y本身的出现频率就很高,也就是说置信度只考虑了“在X发生的条件下Y发生的概率”,但没有考虑Y本身发生的背景概率。它无法区分规则是揭示了一种真正的关联,还是仅仅因为Y本来就非常流行。为了解决这个问题,进一步引入提升度的概念:
- 关联规则x→y的提升度lift(x→y):
。我们可以通过提升度,清晰地判断X和Y之间的关联性质。
| 提升度值 | 数学含义 | 业务解释 | X与Y的关系 |
|---|---|---|---|
| Lift = 1 | P(Y|X) = P(Y) | 购买X,对是否购买Y没有任何影响。Y的发生与X独立 | 相互独立 |
| Lift > 1 | P(Y|X) > P(Y) | 购买X,会提高购买Y的可能性。两者有积极的促进作用 | 正相关 |
| Lift < 1 | P(Y|X) < P(Y) | 购买X,反而降低了购买Y的可能性。两者相互排斥 | 负相关/替代品 |
Apriori算法
apriorifrom typing import Set,List,Tuple import itertools def get_proper_subsets(s): """ 获取集合的所有真子集(不包括空集和集合本身) """ elements = list(s) proper_subsets = [] # 生成长度为 1 到 n-1 的所有组合 for r in range(1, len(elements)): for combo in itertools.combinations(elements, r): proper_subsets.append(set(combo)) return proper_subsets class TransactionTable(list): """ 事务表数据结构 1. 由事务构成,每个事务都是一个集合 2. 提供方法添加单个事务到事务表中 3. 提供方法获取候选1项集 4. 提供方法返回项目在事务表中出现的频率,以及是否频繁 5. 提供方法计算某条关联规则的置信度,以及是否可靠 6. 包含属性最小支持度和最小置信度 7. 提供方法计算提升度 """ def __init__(self,minimum_sup,minimum_con): super(TransactionTable,self).__init__() self.minimum_sup = minimum_sup self.minimum_con = minimum_con def addTransaction(self,transaction:Set): """ 添加一个事项到事项集中 """ assert isinstance(transaction,set),"事务必须是一个集合" self.append(transaction) def getOneCandidates(self): """ 获取候选1项集,返回的是列表的集合 """ assert self,"事务集为空,请首先添加事务" candidates = [] for transaction in self: for item in transaction: if {item} not in candidates: candidates.append({item}) return candidates def getSupport(self,project): """ 计算某个项目集在事项集中出现的频率 """ assert self,"事务集为空,请首先添加事务" counter,frequent = 0,False # 对事项集进行扫描 for transaction in self: # 检查项目集是否在当前事项中出现 if project.issubset(transaction): counter += 1 if counter/len(self) > self.minimum_sup: frequent = True return counter/len(self),frequent def getConfidence(self,project1,project2): """ 计算关联规则project1->project2的置信度 """ reliable = True if self.getSupport(project1|project2)[0]/self.getSupport(project1)[0]>self.minimum_con else False return self.getSupport(project1|project2)[0]/self.getSupport(project1)[0],reliable def getLift(self,project1,project2): return self.getConfidence(project1,project2)[0]/self.getSupport(project2)[0] class Project(set): """ 项目集数据结构 1. 每个项目集都是一个集合,由项目构成,项目可以是任何数据结构的对象 2. 项目集应该包含的属性:是否频繁,每次添加项目后自动更新该属性 3. 提供添加项目的方法 4. 提供方法支持当前项目集和另一个项目集合并后返回一个新的项目集 """ def __init__(self,transaction_table): self.trtable = transaction_table self.sup = None self.frequent = False def addItemBySet(self,a_set): """ 将一个集合或者Project类实例加入当前项目集 """ self.update(a_set) self.sup,self.frequent = self.trtable.getSupport(self) class Rule: """ 关联规则类 """ def __init__(self,trtable,all_rule:List[Tuple]): self.all_rule = all_rule self.trtable = trtable def outputInfo(self): print("从事务表中挖掘出了如下可靠的关联规则:") counter = 0 for rule in self.all_rule: proj1,proj2 = Project(self.trtable),Project(self.trtable) proj1.addItemBySet(rule[0]) proj2.addItemBySet(rule[1]) con,reliable = self.trtable.getConfidence(proj1,proj2) if reliable: print("[{}]:{}->{} with confidence {} and lift {}".format(counter+1,proj1,proj2,round(con,2),\ round(self.trtable.getLift(proj1,proj2),2))) counter+=1 if counter == 0: print("没有达到您要求最小置信度的可靠关联规则") class Apriori: def __init__(self,trtable,verbose=True): self.trtable = trtable # 事务表 self.all_k_project = [] # 所有k项集的集合 self.verbose = verbose def runApriori(self): k = 1 k_candidates = self.trtable.getOneCandidates() for candidate in k_candidates: project = Project(self.trtable) project.addItemBySet(candidate) project.sup,project.frequent = self.trtable.getSupport(project) self.all_k_project.append(project) counter = len([project for project in self.all_k_project if project.frequent]) # 记录频繁k项集的数量 while counter > 0 : # print([(proj,proj.frequent,proj.sup) for proj in self.all_k_project]) # test # 由频繁k项集合组合得到候选k+1项集合 k_plus_candidates = [] for i in range(len(self.all_k_project)-1): for j in range(i+1,len(self.all_k_project)): project = Project(self.trtable) project.addItemBySet(self.all_k_project[i]|self.all_k_project[j]) if len(project) == k+1 and project not in k_plus_candidates: k_plus_candidates.append(project) # 应用定理剪枝 not_frequent_k_candidates = [candidate for candidate in self.all_k_project if not candidate.frequent] for project in k_plus_candidates: for not_freq in not_frequent_k_candidates: if project.issubset(not_freq): not_frequent_k_candidates.remove(project) # 计算支持度 for project in k_plus_candidates: project.sup,project.frequent = self.trtable.getSupport(project) if len([project for project in k_plus_candidates if project.frequent]) == 0: break else: self.all_k_project = [project for project in k_plus_candidates if project.frequent] k = k+1 counter = len(self.all_k_project) # 开始生成关联规则 rules = [] for k_project in self.all_k_project: all_proper_subset = get_proper_subsets(k_project) # 获取真子集 # 两两组合形成规则 for i in range(len(all_proper_subset)): for j in range(len(all_proper_subset)): if not (all_proper_subset[i]&all_proper_subset[j]): rules.append((all_proper_subset[i],all_proper_subset[j])) rules = Rule(self.trtable,rules) if self.verbose: rules.outputInfo() return rules if __name__ == '__main__': # # test1 trtable = TransactionTable(minimum_sup=0.5,minimum_con=0.7) trtable.addTransaction({"苹果","西兰花"}) trtable.addTransaction({"西兰花","大蒜","橙汁","白糖"}) trtable.addTransaction({"苹果","大蒜","橙汁","酱油"}) trtable.addTransaction({"西兰花","苹果","大蒜","橙汁"}) trtable.addTransaction({"西兰花","苹果","大蒜","酱油"}) model = Apriori(trtable) model.runApriori()
这个算法的思路是先去找到项目数量最多的频繁项集,因为这样的项集它的子集也一定是频繁的,可以保证生成的关联规则对应的项集是频繁的,有统计学意义。然后依次获取这些频繁项集的真子集,两两组合得到关联规则,再计算置信度找出强关联规则。
剪枝
Apriori算法需要大量计算项集的支持度,判断项集是否频繁。为了加速,可以使用以下定理快速判断出哪些项集是一定不频繁的,进而减少计算量:
- 频繁项集的子集还是频繁的
- 如果子集不是频繁的那么原项集就不可能是频繁的
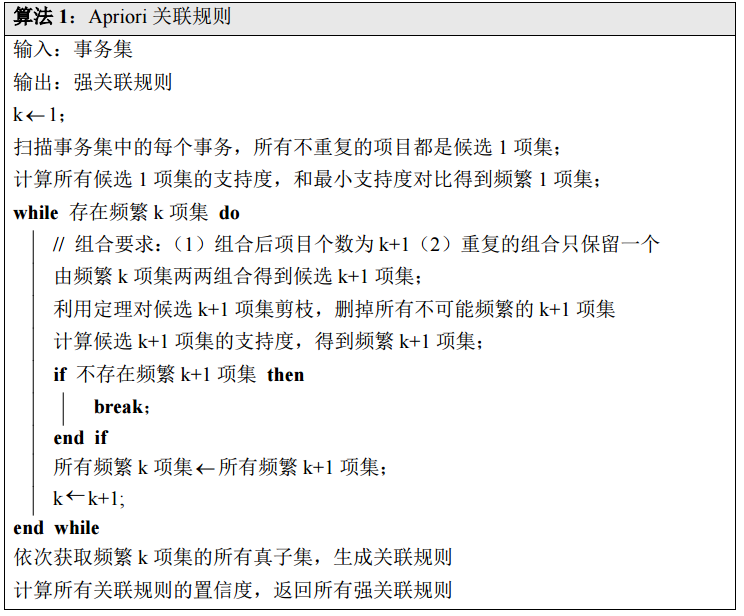
看一个例题,设最小支持度为0.5,最小置信度为0.7,请使用apriori算法得到上述事务表中所有的强关联规则。
| 交易号码 | 商品 |
|---|---|
| 0 | 苹果、西兰花 |
| 1 | 西兰花、大蒜、橙汁、白糖 |
| 2 | 苹果、大蒜、橙汁、酱油 |
| 3 | 西兰花、苹果、大蒜、橙汁 |
| 4 | 西兰花、苹果、大蒜、酱油 |

聚类分析——kmeans算法

kmeans算法import numpy as np from numpy import array,argmin,zeros_like from numpy.linalg import norm from random import sample class Cluseter(list): """ 簇数据结构 1. 是list的子类,包含属性——center,即该簇的中心坐标 2. 提供方法,给定样本坐标返回该样本到这个簇的中心的距离 """ def __init__(self,initial_center): self.center = initial_center def getDistance(self,x): return norm(self.center-x,ord=2) class Kmeans: def __init__(self,data,k): self.data = data self.k = k def runKmeans(self): all_cluster =[] # 获取初始聚类中心,生成初始化的簇 for initial_center in self.data[sample(range(self.data.shape[0]),k=self.k),:]: all_cluster.append(Cluseter(initial_center)) while True: # 计算各个样本到各个聚类中心的距离,将其分配到最近的聚类中心对应的簇 for x in self.data: distances = [] for cluseter in all_cluster: distances.append(cluseter.getDistance(x)) pos = argmin(distances) all_cluster[pos].append(x) # 加入最距离最近的簇 # 重新计算各个簇的中心 old_center = [] for cluster in all_cluster: new_center = zeros_like(cluster.center) old_center.append(cluseter.center) for x in cluster: new_center += x cluster.center = new_center/len(cluster) flag = False # 假设中心没有发生变化 # 检查中心是否变化 for i in range(len(all_cluster)): if sum(abs(all_cluster[i].center-old_center[i])) > 1e-5: break flag = True if not flag: return all_cluster if __name__ == '__main__': data = array([[1,1],[2,2],[2,3],[3,2],[6,3],[6,1],[7,2]]) model = Kmeans(data,k=2) all_cluster = model.runKmeans() print(all_cluster)
看一个例题,给定含有4个样本的集合
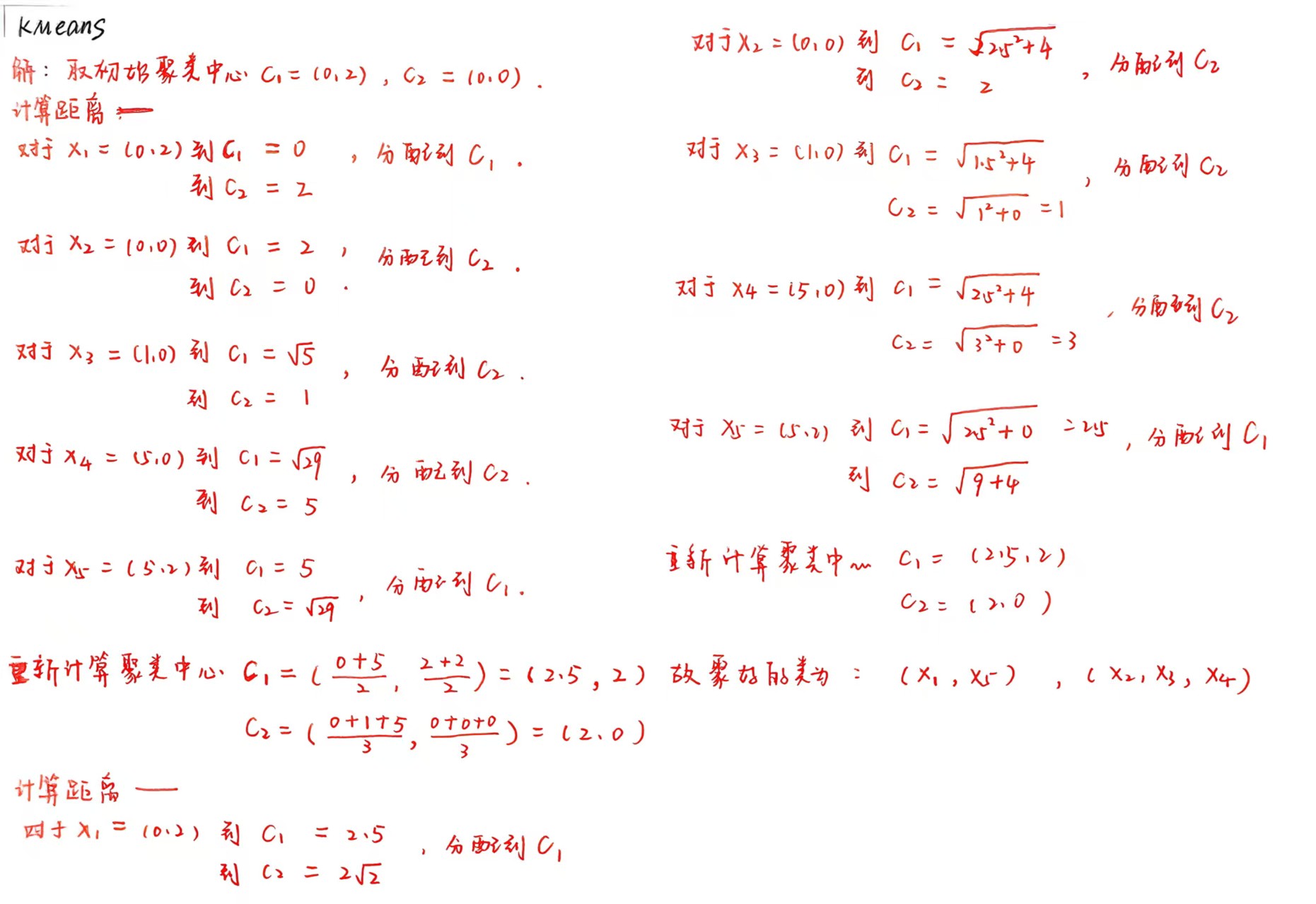
优化算法部分
算法描述方法——伪代码

优化算法评价
优化算法评价分为三个部分:时间性能评价、近似性能评价和鲁棒性能评价。
时间性能评价——时间复杂度分析
设问题输入规模是n,时间复杂度可以用语句频度
: 的一个上界是 ,在时间复杂度分析中上界的定义是——若存在 使得 有 成立,则称 的一个上界是 : 和 是同阶的,在时间复杂度分析中同阶的定义是——若存在 使得 有 成立,则称 的一个同阶是 : 的一个下界是 ,在时间复杂度分析中下界的定义是——若存在 使得 有 成立,则称 的一个下界是
下面看一个例题,分析这个算法的时间复杂度:

近似性能评价
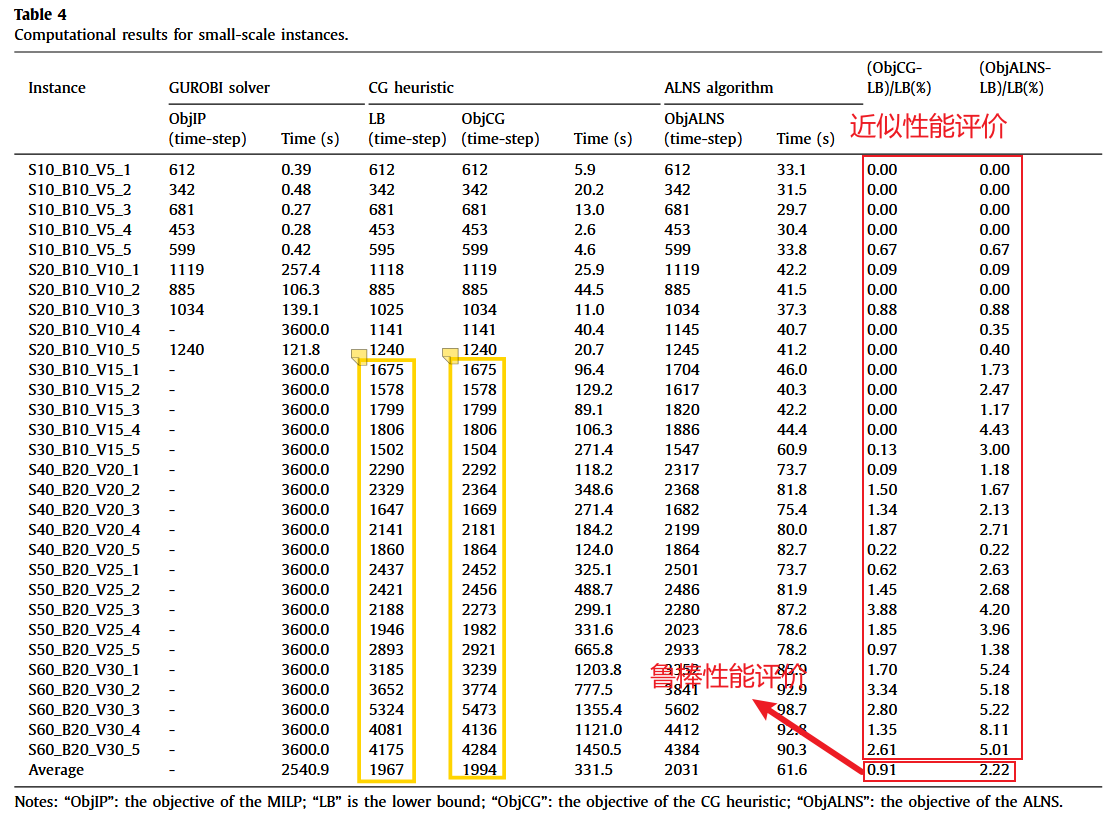
算法近似性能的评估通常是通过实验完成。包括在线Gap和离线Gap,所谓在线Gap就是你调用gurobi用分支切割算法的时候控制台输出的那个gap,它是算法当前找到的最优解目标函数值和问题下界的偏差,在论文里面经常用的是离线Gap,也就是等算法运行完后,去看找到的最优解目标函数值和下界的偏差,例如刘保利老师21年的这篇文章。
鲁棒性能评价
就是在不同的算例上看算法的运行效果,还是刘保利老师21年的文章,最后一行给在各个算例上的平均gap就算是鲁棒性能评价。
P、NP、NPC和NP-hard
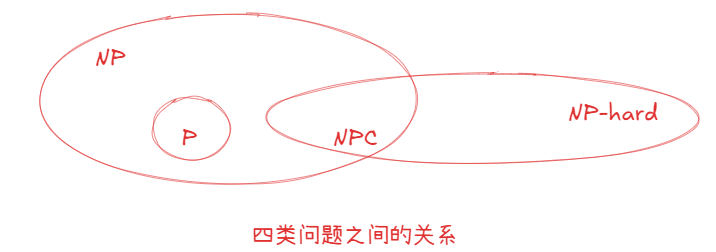
任何一个待求解的问题都可以分为以下四类:
- P问题:存在多项式时间算法求解的问题,很简单。
- NP问题:存在多项式时间算法验证一个解的正确性,但是不确定有没有多项式时间算法可以解这个问题。
- NPC问题:(1)是NP问题(2)所有NP问题都可以规约为它,也就是所有NP问题都没它难。
- NP-hard问题:所有NP问题都可以规约为它,也就是所有NP问题都没它难。
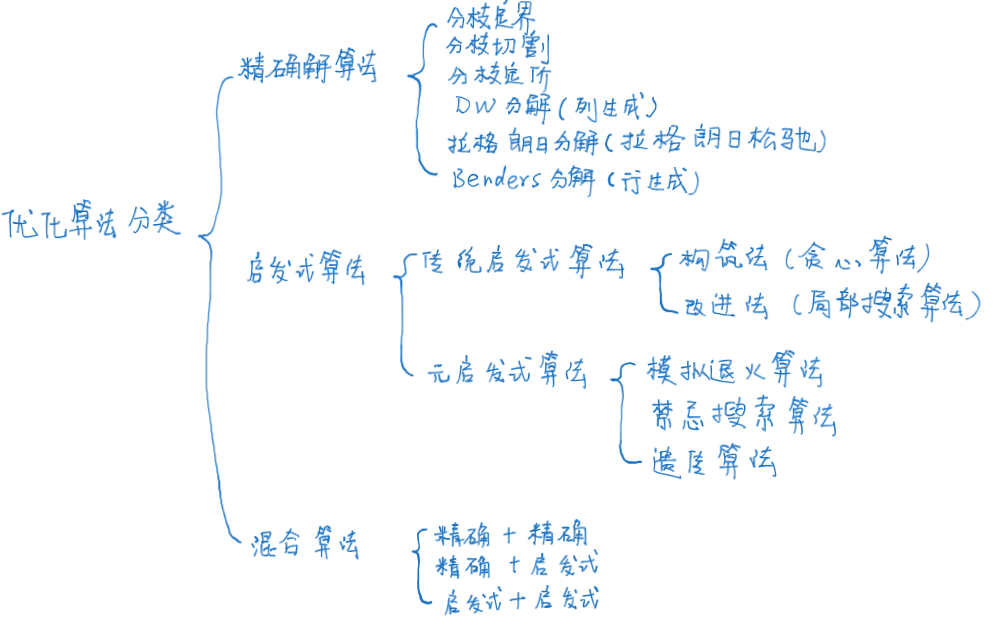
关于求解方法选择
Np是否等于p是一个悬而未决的问题,但目前主流观点认为是不等的,所以要求解特别大规模的Np基本就得往启发式算法上面考虑了,NPC和NP-hard比NP问题还难,同理。
传统启发式
贪心算法(构筑算法)
构筑法就是从头开始构造出一个解,一般是使用贪心的思想,即构造的每一步都做当下最有利的选择。如下使用构筑法得到tsp问题的一个解。

局部搜索算法(改善算法)
所谓改善算法实际上就是局部搜索算法(大部分元启发式算法的爹),思路就是从一个初始解开始,探索邻域,转换为更好的解,直到找不到更好的解。局部搜索算法这块最重要的就是掌握一些邻域操作,常见的邻域操作如下:
- tsp的2-opt交换: 2-opt交换就是两步,第一步找到两个不相邻的边,然后断开这两条边重新连接。假设我们有一个路径(访问顺序)A → B → C → D → E → F → A,选择路径中不相邻的两条边A → B和D → E,断开A → B和D → E,连接A → D和B → E,为了保证路径的连贯性,进一步反转B → D之间路径的顺序。
- tsp的or-opt插入:任选一个子路径插入到某一个点之后。
- vrp的insert-opt插入:将另一车辆路径上的城市插入到当前车辆路径某个客户点之后。
- vrp的cross-opt交换:将两个车辆路径的某个子路径进行交换。
补充:局部探索策略
局部搜索算法是包含两种策略的,第一种是最初改善策略,就是说一旦在邻域找到更好的点就移动到这个点,在探索这个点的邻域;第二种策略是最大改善策略,就是说先把当前点的邻域“看完”,最后再移动到这个点邻域最好的那个点上。后面可以看到,模拟退火的局部搜索部分实际上用的是最初改善策略,而禁忌搜索算法的局部搜索部分用的是最大改善策略。
元启发式
关于元启发式的一个观点
基本上所有元启发式算法的思想都是局部搜索+跳出局部最优的机制,不同元启发式之间的核心差异在于它们跳出局部最优的机制是什么。
模拟退火
模拟退火算法(Simulated Annealing,SA)是一种启发式搜索算法,它借鉴了物理学中固体退火的原理。退火过程中,固体被加热至高温,使得其内部粒子处于无序状态并拥有较高的内能。随后,固体缓慢冷却,粒子逐渐有序排列,内能降低,最终在常温下达到能量最低的基态。模拟退火算法利用这一原理,在求解优化问题时,通过模拟退火过程来寻找全局最优解。

关于目标函数的标定
模拟退火算法和遗传算法类似,里面也涉及到目标函数的标定问题,目标函数值越好则对应的能量值应该越低。
模拟退火#!/usr/bin/env python # -*- coding: utf-8 -*- # @Date : 2025-12-15 20:18:10 # @Author : syuansheng (Dalian Maritime University) """ 模拟退火算法 """ import math import random import copy class Problem: def get_energy(self,solution): # 目标函数和能量的标定过程,解越好,能量越低,对于min问题,直接可以用目标函数作为能量 return 4*solution[0]**2-2.1*solution[0]**4+solution[0]**6/3+solution[0]*solution[1]-4*solution[1]**2+4*solution[1]**4+\ 999*max(0,solution[0]-5)-999*min(0,solution[0]+5)+\ 999*max(0,solution[1]-5)-999*min(0,solution[1]+5) def get_initial_solution(self): return [random.randint(-5,5),random.randint(-5,5)] def local_search(self,solution): # 这里就做个微小扰动实现局部搜索 solution = copy.deepcopy(solution) # 这一块儿非常坑,你传进来参数,python就获得了对那个对象的应用,必须深拷贝才不会干扰 solution[0] = solution[0] + random.randint(-1,1)*random.random() solution[1] = solution[1] + random.randint(-1,1)*random.random() return solution class SimulatedAnnealingSolver: def __init__(self,T0:float,Tf:float,L:int=100)->None: self.T0 = T0 # 初始温度 self.Tf = Tf # 终止温度 self.L = L # 恒温迭代次数(马尔科夫链长度) def solve(self,problem): # 模拟退火算法框架 current_x = problem.get_initial_solution() best_x = current_x current_T = self.T0 while current_T > self.Tf: # 恒温过程 for iteration in range(self.L): new_x = problem.local_search(current_x) energy_current_x = problem.get_energy(current_x) energy_new_x = problem.get_energy(new_x) # metropolis准则 if energy_new_x-energy_current_x < 0: current_x = new_x else: p = math.exp(-(energy_new_x-energy_current_x)/current_T) if random.random() < p: current_x = new_x if problem.get_energy(current_x) < problem.get_energy(best_x): best_x = current_x # 指数降温公式 current_T = current_T*0.999 print('当前温度:{},能量值:{},最优解:{}'.format(current_T,problem.get_energy(best_x),best_x)) return best_x if __name__ == '__main__': problem = Problem() solver = SimulatedAnnealingSolver(T0=50,Tf=1) solver.solve(problem)
禁忌搜索
禁忌搜索算法(Tabu Search,TS)是由美国数学家 Fred Glover 在20世纪80年代提出的一种元启发式搜索算法。它是一种局部搜索的扩展,通过引入禁忌机制以及确定性地劣解接受机制来避免陷入局部最优解。禁忌搜索算法的灵感来源于人类的思考过程,当我们遇到问题时,会尝试不同的解决方案,如果某个方案被证明是无效的,我们就会把它标记为禁忌,不再轻易尝试。
禁忌搜索和模拟退火的核心区别
它们在思路上都是局部搜索+跳出局部最优的机制。差异就在跳出局部最优的机制上面,模拟退火是通过按概率接受劣解跳出局部最优,而禁忌搜索是通过取邻域的一个子集,然后确定性的接受该子集中的某个解(可能更好,可能更差)来跳出局部最优。

禁忌搜索算法#!/usr/bin/env python # -*- coding: utf-8 -*- # @Date : 2025-12-15 21:58:14 # @Author : syuansheng (Dalian Maritime University) """ 禁忌搜索算法:与模拟退火算法的最大区别在于如何跳出局部最优,模拟退火算法是对当前解的邻域采样,然后通过按概率接受劣解跳出局部最优,而 禁忌搜索确定性地是对当前解的邻域进行多次采样,然后从里面选最好的(可能比当前解差,也可能比当前解好)的解作为当前解。 禁忌表存在的目的是为什么避免在邻域的某些点循环搜索 """ from numpy import argmin from random import shuffle,sample from copy import deepcopy from math import inf class Problem: def __init__(self,distances): self.distances = distances # 各个点的坐标 def get_initial_solution(self): s = list(range(100)) shuffle(s) return s def greedy_initial_solution(self): """ 使用贪心法构造初始解 """ s = [0] while True: temp = self.distances[s[-1],:] # 当前点到其余各个点的距离 pos = None # 下一个点 dis = inf for i in range(len(temp)): if i not in s and temp[i]<dis: pos = i dis = temp[i] s.append(pos) if len(s) == 99: s.append(0) return s def get_obj(self,x): obj = 0 # 取相邻两个位置 for i,j in zip(range(99),range(1,100)): obj += self.distances[x[i],x[j]] return obj def get_candidate(self,x): # 随机选择两个点做交换 pos1,pos2 = sample(range(100),k=2) move = (pos1,pos2) x_cadi = deepcopy(x) x_cadi[pos1],x_cadi[pos2] = x_cadi[pos2],x_cadi[pos1] obj = self.get_obj(x_cadi) return move,x_cadi,obj class TabuSearchSolver: def __init__(self,num_candidates:int=50,length:int=13,max_iter:int=1000): self.num_candidates = num_candidates # 候选解的个数(探索某点整个邻域不现实,只从他的邻域中取num_candidates个) self.length = length # 禁忌表的长度,决定一个移动多少次迭代被禁止使用 self.max_iter = max_iter # 算法的最大迭代步数 def solve(self,problem): L = [] # 禁忌表 current_x = problem.greedy_initial_solution() # 获取一个初始解,current_x实际上指的就是局部最优解,best_x指的是最好的局部最优解,不不不,这个说法不对,current_X也不一定是局部最优的 best_x = current_x for iteration in range(self.max_iter): # 获取候选移动的集合,及其对应的候选解、候选解的目标值 move_candidates,x_candidates,obj_candidates = [],[],[] for _ in range(self.num_candidates): move,x,obj = problem.get_candidate(current_x) # 根据当前解获取一个移动及其对应的候选解以及目标值 move_candidates.append(move) x_candidates.append(x) obj_candidates.append(obj) # 检查一下是否要使用特赦规则:移动虽然被禁掉了,但是使用这个移动直接能得到比x_best更好的解,那就特赦 for move,x,obj in zip(move_candidates,x_candidates,obj_candidates): if move in L: if obj < problem.get_obj(best_x): current_x = x best_x = x break # 没有使用特赦,确定性的接受候选解集合中的最好解(可能比当前解好,也可能比当前解x_cur差)这是禁忌搜索跳出局部最优的核心机制 else: # 寻找到不在禁忌表中的最好解(可能比当前解好,也可能比当前解x_cur差) pos = 0 guess = inf for i in range(len(obj_candidates)): if obj_candidates[i] < guess and move_candidates[i] not in L: pos = i guess = obj_candidates[i] current_x = x_candidates[pos] L.append(move_candidates[pos]) # 把对应移动加入禁忌表 if len(L) > self.length: L.pop(0) # 解禁 if problem.get_obj(current_x)<problem.get_obj(best_x): best_x = current_x print('iteration:{},obj/10^6:{}'.format(iteration,problem.get_obj(best_x)/10**6)) return best_x def calculate_distance(city_locations): r= 6371*1e3 # 地球半径m distances=zeros((len(city_locations),len(city_locations))) # 101x101的实对称数组,存储i到j的距离 longitude,latitude=city_locations[:,0],city_locations[:,1] for i in range(len(city_locations)): for j in range(len(city_locations)): phi1 = math.radians(latitude[i]) phi2 = math.radians(latitude[j]) delta_phi = math.radians(latitude[j] - latitude[i]) delta_lambda = math.radians(longitude[j] - longitude[i]) a = math.sin(delta_phi / 2) ** 2 + math.cos(phi1) * math.cos(phi2) * math.sin(delta_lambda / 2) ** 2 c = 2 * math.atan2(math.sqrt(a), math.sqrt(1 - a)) distance=r*c # 通过经纬度计算地球上两点距离的公式 distances[i,j]=distance return distances if __name__ == '__main__': import math from numpy import array,zeros position = array([ [53.7121, 15.3046, 51.1758, 0.0322, 46.3253, 28.2753, 30.3313, 6.9348], [56.5432, 21.4188, 10.8198, 16.2529, 22.7891, 23.1045, 10.1584, 12.4819], [20.1050, 15.4562, 1.9451, 0.2057, 26.4951, 22.1221, 31.4847, 8.9640], [26.2418, 18.1760, 44.0356, 13.5401, 28.9836, 25.9879, 38.4722, 20.1731], [28.2694, 29.0011, 32.1910, 5.8699, 36.4863, 29.7284, 0.9718, 28.1477], [8.9586, 24.6635, 16.5618, 23.6143, 10.5597, 15.1178, 50.2111, 10.2944], [8.1519, 9.5325, 22.1075, 18.5569, 0.1215, 18.8726, 48.2077, 16.8889], [31.9499, 17.6309, 0.7732, 0.4656, 47.4134, 23.7783, 41.8671, 3.5667], [43.5474, 3.9061, 53.3524, 26.7256, 30.8165, 13.4595, 27.7133, 5.0706], [23.9222, 7.6306, 51.9612, 22.8511, 12.7938, 15.7307, 4.9568, 8.3669], [21.5051, 24.0909, 15.2548, 27.2111, 6.2070, 5.1442, 49.2430, 16.7044], [17.1168, 20.0354, 34.1688, 22.7571, 9.4402, 3.9200, 11.5812, 14.5677], [52.1181, 0.4088, 9.5559, 11.4219, 24.4509, 6.5634, 26.7213, 28.5667], [37.5848, 16.8474, 35.6619, 9.9333, 24.4654, 3.1644, 0.7775, 6.9576], [14.4703, 13.6368, 19.8660, 15.1224, 3.1616, 4.2428, 18.5245, 14.3598], [58.6849, 27.1485, 39.5168, 16.9371, 56.5089, 13.7090, 52.5211, 15.7957], [38.4300, 8.4648, 51.8181, 23.0159, 8.9983, 23.6440, 50.1156, 23.7816], [13.7909, 1.9510, 34.0574, 23.3960, 23.0624, 8.4319, 19.9857, 5.7902], [40.8801, 14.2978, 58.8289, 14.5229, 18.6635, 6.7436, 52.8423, 27.2880], [39.9494, 29.5114, 47.5099, 24.0664, 10.1121, 27.2662, 28.7812, 27.6659], [8.0831, 27.6705, 9.1556, 14.1304, 53.7989, 0.2199, 33.6490, 0.3980], [1.3496, 16.8359, 49.9816, 6.0828, 19.3635, 17.6622, 36.9545, 23.0265], [15.7320, 19.5697, 11.5118, 17.3884, 44.0398, 16.2635, 39.7139, 28.4203], [6.9909, 23.1804, 38.3392, 19.9950, 24.6543, 19.6057, 36.9980, 24.3992], [4.1591, 3.1853, 40.1400, 20.3030, 23.9876, 9.4030, 41.1984, 37.7349] ]).reshape(-1,2) distances = calculate_distance(position) problem = Problem(distances) tssolver = TabuSearchSolver(500,max_iter=1000,length=6) tssolver.solve(problem)
遗传算法

常见混合算法
- 精确解算法与精确解算法混合
- 精确解算法和启发式算法混合
- 启发式算法和元启发式算法混合
- 元启发式和元启发式混合






.png)